assalamualaikum semuanya? apa kabar? saya harap kalian sehat selalu dan tetap semangat dalam beraktivitas. di kesempatan kali ini saya akan membahas tentang MATRIKS, mungkin dari kalian sudah ada yang tahu pelajaran ini di bangku SMK atau SMA. okeh kali ini tidak perlu basa basi mari saya jelaskan apa sih itu MATRIKS secara singkat dan insa allah dapat dipahami.
okeh langsung saja kita mulai dari pengertiannya terlebih dahulu....
PENGERTIAN
Matriks adalah susunan bilangan-bilangan riil atau kompleks yang diatur dalam baris-baris dan kolom-kolom berbentuk persegi panjang. Bilangan-bilangan tersebut disebut elemen matriks. Cara penulisan kolom matriks adalah sebagai berikut (dengan angka) :

Matriks dinyatakan dalam huruf besar A, B, P atau huruf yang lainnya. Atau secara lengkap ditulis A = (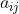 ), artinya matriks A mempunyai elemen
), artinya matriks A mempunyai elemen 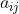 , dimana indeks i menyatakan baris ke-i dan indeks j menyatakan kolom ke-j dari elemen aij. Secara umum, matriks A ditulis : A = (
, dimana indeks i menyatakan baris ke-i dan indeks j menyatakan kolom ke-j dari elemen aij. Secara umum, matriks A ditulis : A = (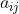 )
)

Matriks A mempunyai baris sebanyak n dan kolom sebanyak m. Pada
matriks A = , dikatakan ordo matriks A adalah m x n.
, dikatakan ordo matriks A adalah m x n.
matriks A =

hayoo sudah ada yang sudah mulai paham?? di simak kembali ya bila belum paham, kita lanjut kebagian pengoperasian MATRIKS
OPERASI MATRIKS
Selanjutnya kita akan mempelajari apa saja operasi-operasi di dalam Matriks.
Dalam operasi matriks terdapat beberapa sifat matriks jika matriks A, B
dan C berordo sama dan λ scalar, maka berlaku sifat-sifat berikut:
dan C berordo sama dan λ scalar, maka berlaku sifat-sifat berikut:
a. A + B = B + A (sifat komutatif)
b. (A + B) + C = A + ( B + C); (sifat asosiatif)
c. λ(A + B) = λA + λB; (sifat distributif)
b. (A + B) + C = A + ( B + C); (sifat asosiatif)
c. λ(A + B) = λA + λB; (sifat distributif)
1. Operasi penjumlahan dan pengurangan
Jumlah matriks A dan B jika ditulis A + B adalah sebuah matriks baru C, C = A + B dengan elemen =
= 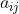 +
+ , i = 1,2,…,m dan j = 1,2,…,n dengan syarat A dan B
, i = 1,2,…,m dan j = 1,2,…,n dengan syarat A dan B
mempunyai ordo sama. Jadi matriks C = ( ) = (
) = (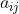 +
+ ).
).
Jumlah matriks A dan B jika ditulis A + B adalah sebuah matriks baru C, C = A + B dengan elemen
mempunyai ordo sama. Jadi matriks C = (
Contohnya seperti gambah dibawah ini ⇓

3A – B=

2. Perkalian Skalar / bilangan dengan matriks
Bila λ suatu bilangan dan a =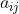 maka perkalian λ dengan A ditulis A = λ(
maka perkalian λ dengan A ditulis A = λ(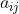 ) = (λ
) = (λ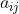 ), atau dengan kata lain matriks λA diperoleh dari perkalian semua elemen A dengan λ.
), atau dengan kata lain matriks λA diperoleh dari perkalian semua elemen A dengan λ.
Bila λ suatu bilangan dan a =
berikut adalah contoh soal ⇓

3. Transpose Matriks
Bila matriks A = (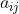 ), berordo (mxn), maka transpose dari matriks A ditulis
), berordo (mxn), maka transpose dari matriks A ditulis  adalah matriks yang diperoleh dari A dengan menukar semua baris matriks A menjadi kolom
adalah matriks yang diperoleh dari A dengan menukar semua baris matriks A menjadi kolom
matriks . Maka matriks
. Maka matriks  akan berordo nxm.
akan berordo nxm.
Bila matriks A = (
matriks
Agar mudah dipahami mari kita lihat contoh soal di bawah ⇓

4. Operasi Perkalian
Bila A = (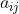 ) berorodo (pxq) dan matriks B = (
) berorodo (pxq) dan matriks B = ( ) berordo (qxr), maka perkalian matriks A dan B ditulis AxB, adalah matriks C = AxB = (
) berordo (qxr), maka perkalian matriks A dan B ditulis AxB, adalah matriks C = AxB = ( ) berordo (pxr), dimana
) berordo (pxr), dimana  =
=  +
+
 +..….+
+..….+ 
Syarat agar matriks A dan B bisa dikalikan adalah banyaknya kolom matriks A harus sama dengan banyaknya baris matriks B.
Contohnya ⇓

5. Jenis-Jenis Matriks
i. Matriks bujur sangkar, apabila suatu matriks memiliki jumlah baris dan kolom sama, atau berordo nxn.
Contohnya bisa dilihat dibawah ini ⇓

ii. Matriks nol, adalah matriks yang semua elemennya sama dengan nol.
Contohnya ⇓

iii. Matriks diagonal, adalah matriks bujur sangkar yang semua elemen diluar diagonal utama sama dengan nol.
Contohnya ⇓

iv. Matriks satuan (identitas), ditulis dengan I adalah matriks bujur sangkar yang elemen diagonalnya semua sama dengan 1, dan elemen yang lain sama dengan 0.
Contohnya ⇓

v. Matriks simetris, adalah matriks yang transposenya sama dengan dirinya sendiri atau A =  .
.
Contohnya ⇓

vi. Matriks segitiga bawah adalah matriks bujur sangkar yang semua elemen diatas diagonal utama adalah 0.
Contohnya ⇓

Sekian dulu untuk pembahasan matriks kali ini. Semoga melalui pembahasan ini kita menjadi paham mengenai pelajaran tentang matriks dan semoga bermanfaat untuk kalian yang sudah mampir di blog saya ini, terima kasih sudah mampir :)
Tidak ada komentar:
Posting Komentar